<< prev story                                circuit-fantasia > circuit stories > understanding circuits > simple BJT current source                                  next story >>

 

What is the idea behind this circuit?

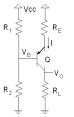
Simple BJT Current Source

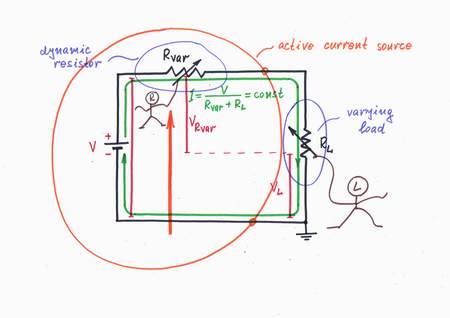
Idea: Keeping a constant current by varying the internal resistance.

In order to keep a constant current, we may change Ri (Rvar) to the opposite direction thus keeping a constant total circuit resistance Rtot = Rvar + RL = const. Click to view full-size picture.

The simple current source is imperfect as the load affects the current. For example, let's the load has varying ohmic resistance RL. As the source has a constant internal resistance Ri, the total circuit resistance Rtot = Ri + RL will vary. As a result, the current I will vary as well. How to solve the problem?

According to the basic idea above, we change Rvar to the opposite direction thus keeping a constant total circuit resistance Rtot = Rvar + RL = const. Rvar acts as a resistor with dynamic resistance, which complements RL to Rtot. As a result, a constant current flows through the load.

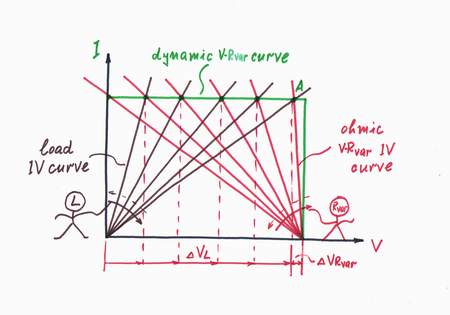
The two IV characteristics rotate in opposite directions. As a result, the working point A slides horizontally over dynamic IV curve of the current-stable resistor Rvar. Click to view full-size picture.

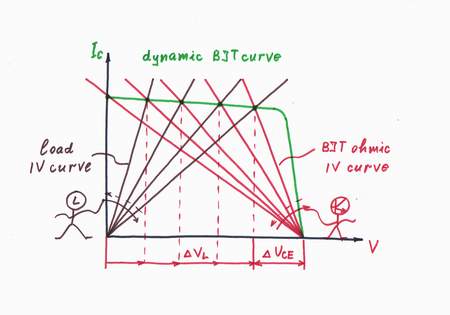
Graphically presented, when the load increases its resistance, the IV curve rotates clockwise round the zero of the coordinate system. The resistor Rvar reacts to this intervention by decreasing its resistance and rotating contraclockwise the IV curve. As a result, the working point A slides horizontally over the dynamic IV curve of the current-stable resistor Rvar.

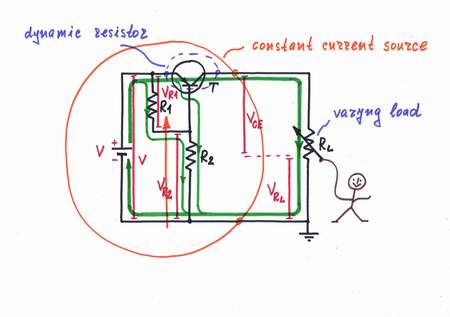
Implementation: Using a bipolar transistor as a varying (dynamic) resistor.

In the simple BJT current source, the transistor acts just as a varying resistor Rvar. Click to view full-size picture.

Just this idea is applied in the circuit of the simple BJT constant current source. Here a bipolar transistor is connected in series with the load. The voltage divider R1-R2 sets a constant input voltage on the transistor base. As a result, the transistor acts just as a varying resistor Rvar: when the load varies, the transistor changes its present resistance RCE to the opposite direction in order to keep a constant total circuit resistance Rtot = RCE + RL.

Doing this magic, the transistor actually functions as a current-stable dynamic resistor and the whole circuit acts as a constant current source.

The two IV characteristics rotate in opposite directions. As a result, the working point A slides horizontally over dynamic IV curve of the transistor T. Click to view full-size picture.

As before, when the load increases its resistance, the IV curve rotates clockwise round the zero of the coordinate system. The transistor T reacts to this intervention by decreasing its static resistance and rotating contraclockwise the IV curve. As a result, the working point A slides horizontally over the dynamic IV-curve of the transistor.

<< prev story                                circuit-fantasia > circuit stories > understanding circuits > simple BJT current source                                  next story >>