Inventing Circuits on the Whiteboard...

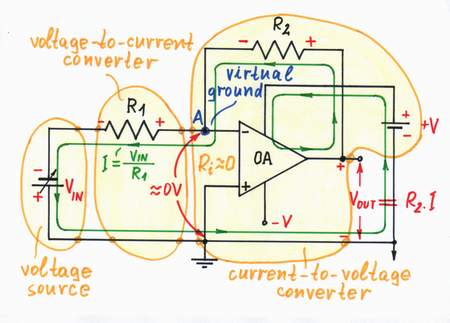
How to Transform the Passive Current-to-Voltage Converter into an Active One

Circuit idea: The op-amp compensates the internal losses caused by the resistor adding as much voltage to the input voltage source as it loses across the resistor.

Speculation: Is the active version just an improved passive one?

We have already revealed the secret of the most popular simple converting circuit - passive current-to-voltage converter. We know that these kinds of circuits have usually two versions - passive ("bad") and active ("good"). When we were considering the opposite voltage-to-current converter, we ascertained that there was a close interrelation between the two versions - the active circuit was come from the passive one; it was just an improved passive version. Furthermore, we figured out how the passive version was transmuted into an active one.

Similarly, we may now suppose that there is an active current-to-voltage converter and its passive and active versions are interrelated too. Then, let's look at these two circuit implementations - the "bad" passive version (the top of the small picture above) and the "good" active version (the bottom of the picture). We can see again that the active version contains the passive one + an op-amp connected in accordance with some (maybe the same?) powerful idea:

Active I-to-V converter = passive I-to-V one + op-amp + great idea ?

Again, we might ask ourselves, "How have the passive circuit transmuted into an active one?", "What is the idea of this connection?" and "What does the op-amp do in this circuit?" We can answer these questions by following the evolution of the passive circuit into an active one.

Internal links:

1.   Problem: The internal resistor affects the current

2.   Basic idea: Removing a disturbance by an "antidisturbance"

3.   Basic electrical idea: Removing a voltage by an "antivoltage"

4.   Exploring the active circuit

5.   Creating an op-amp inverting voltage-to-current converter

6.   Exploring the circuit at positive input voltage

7.   Exploring the circuit at negative input voltage

8.   Applications: Staying before the circuit input

9.   Applications: Staying after the circuit output

10.  Comparison between the passive and active version

Color key

Links:  this page, other my pages, external, multimedia, handmade.

Text:   analogies, conclusions.

Problem: The internal resistor affects the current

top < prev step - 1 - 2 - 3 - 4 - 5 - 6 - 7 - 8 - 9 - 10 - next step > end

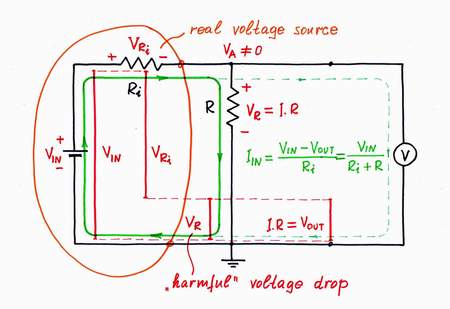
We have already known why the simple current-to-voltage converter is an imperfect circuit - because the output voltage drop VR across the internal resistor R affects the input current (here we suppose that the input current is created by a real source consisting of a voltage source VIN and an internal resistance Ri).

We can look at the voltage VR from two contrary viewpoints. From the point of view of the input voltage source, the voltage drop VR is troublesome; so, the input source "would like" this voltage not to exist. Contrary, from the point of view of the load, VR is a useful voltage drop as it serves as an output quantity; so, the load "would like" this voltage to exist and even it to be as much as possible high. Obviously, there is a contradiction here - the voltage drop VR has to exist and, at the same time, not to exist. How do we solve this contradiction?

You can explore the operation of the passive circuit in a more attractive way, if you click Exploring button in the interactive flash movie or if you go to Stage 2 in the interactive flash builder.

Basic idea: Removing a disturbance by an "antidisturbance"

top < prev step - 1 - 2 - 3 - 4 - 5 - 6 - 7 - 8 - 9 - 10 - next step > end

Remember what we do in real life when we solve some problem but a disturbance caused by ourselves stands in our way. The classical remedy is to remove the cause of the disturbance. Only, it is not always possible to do that; then, we use another exotic solution - we remove the disturbance by an equivalent "antidisturbance". For this purpose, we use an additional power source (energy), which "helps" us (the main source) by compensating only the local losses caused by the internal troublesome quantity (conversely, in the opposite active voltage-to-current converter, the additional power source compensates the losses caused by the external quantity).

This technique is associated with continuous wasting of additional energy but the result is zero (virtual ground); so, we prefer to use it when we are rich and, at the same time, lazy enough:). An example: if we have broken our window in winter, we turn on a heater that compensates the thermal losses; and v.v., in summer, we turn on an air-conditioner.

More examples: if our car has come into collision with other car, the insurance company compensates the damages that we have caused to the else's car, if we cause troubles to others, we apologize, if we have spent money from our account, we begin depositing additional money into the account, etc. (see virtual ground wiki page for more examples).

In all these cases, we have prepared (just in case) "standby" resources to use them, if there is a need to compensate eventual internal losses.

Basic electrical idea: Removing a voltage by an "antivoltage"

top < prev step - 1 - 2 - 3 - 4 - 5 - 6 - 7 - 9 - 10 - next step > end

Now, let us put this powerful idea into practice. The voltage drop VR across the resistor R is harmful; so, following the recipe above, we have to remove it by an "antivoltage" -VR. In other words, we have to add so much voltage to the input (excitation) voltage source VIN, as much as it loses across the resistor R:

Active I-to-V converter = passive one + "helping" voltage source

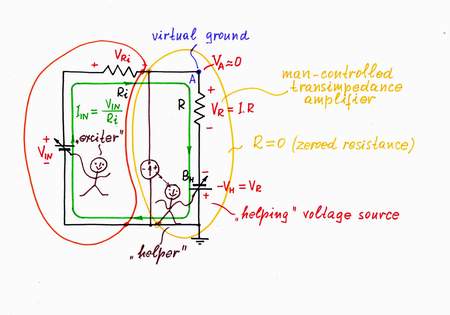
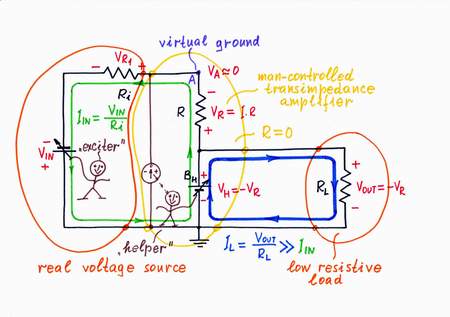
The best way to understand what real electronic components do is just to do their work. So, let us first build a "man-controlled" active circuit, in which a man (I might do this donkeywork:) produces the "anti-voltage" while you change the input voltage. For this purpose, I first place an additional supplementary battery BH in series to the resistor R. Then, in order to compare the two voltages, I connect a zero indicator in point A, which shows the result of comparison VA = VH - VR. See how simple it is:

Add an adjustable battery in series with the resistor and make its voltage equal to the voltage drop across the resistor!

Building a "man-controlled" electrical circuit

Now, we have to decide where to take the output (where to connect the load). Let's consider the possible solutions.

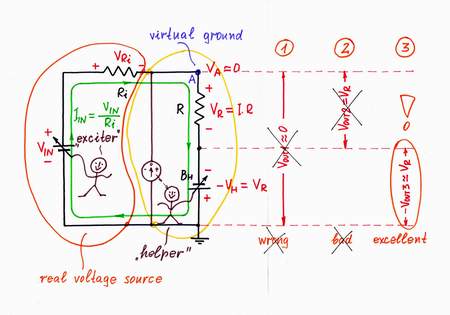
VOUT1 = VA = 0. It is naturally to try using the old circuit output (the voltage of point A versus the ground). But we have just destroyed this voltage (the point A has become virtual ground)! So, we can't use this voltage as an output:(

VOUT2 = VR. Then let's try using the voltage VR across the resistor R. Only, in order to connect a load to the "floating" resistor R, the load has to have a differential input. Moreover, if the load has some resistance, it will shunt the resistor thus affecting the current. What do we do then? Here is a tip.

Recall to mind the cases from our routine when we prefer to estimate indirectly some quantity X. For this purpose, we first destroy the unknown quantity by an equal "anti-quantity" Y = X; then, we measure the "anti-quantity" Y, in order to know the magnitude of the initial quantity X. An example - classic weighing by using balance.

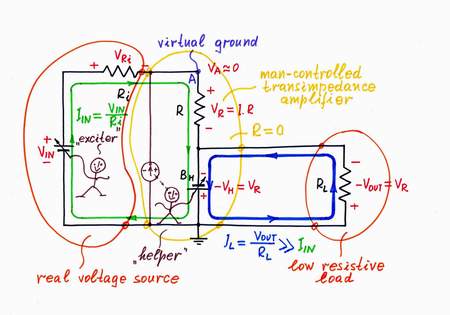
VOUT3 = -VH. Eureka! We will use the "copy" voltage -VH as an output instead the "original" voltage VR! What a great idea! In this case: first, the load will be connected to the common ground; second, it will consume energy from the "helping" source BH instead from the input source VIN!

Where to take an output from?

Exploring the active circuit

It's time to explore the circuit operation. In the beginning, imagine that there is not input excitation voltage VIN (see again the figure above). As a result, there are not any voltage drops and currents in the circuit; the needle of the zero indicator points to zero position. I am happy because there is nothing to do:)

top < prev step - 1 - 2 - 3 - 4 - 5 - 6 - 7 - 8 - 9 - 10 - next step > end

If you increase the input voltage VIN, a current begins flowing through the resistor. As a result, a voltage drop VR appears across the resistor and the point A begins rising its potential VA (figuratively speaking, the input source "pulls" the point A up toward the positive voltage VIN). Only, I observe to my great displeasure:( that the needle deflects to the right and immediately react by decreasing the compensating voltage VH. Now, it "pulls" the point A down toward the negative voltage -VH until it manages to zero the potential VA (the virtual ground). Note that the two voltage sources are connected in series, in one and the same direction (- VIN +, - VH +) so that their voltages are added (let us assume that we traverse the loop clockwise). Regarding to the ground, they have opposite polarities.

In this way, the input voltage source is "helped"; its voltage increases so much (VIN) as it loses across the load. As a result, the "disturbing" voltage VR disappears; the point A has zero voltage; it behaves as a virtual ground. The real input voltage source is "fooled": it has the illusion that its output is shorted.

How the active current-to-voltage converter operates (+VIN)

If you decrease the input voltage VIN under the ground, an input current IIN begins flowing through the resistor R in an opposite direction. As a result, a voltage drop VR appears across the resistor R and the point A begins dropping its potential VA (now, the input source "pulls" the point A down toward the negative voltage -VIN). Only, I observe that the needle deflects to the left and immediately react by increasing the compensating voltage VH. Now, it "pulls" the point A up toward the positive voltage VIN until it manages to zero again the potential VA (virtual ground). The two voltage sources are connected in series again, in one and the same direction (+ VIN -, + VH -) so that their voltages are added. Regarding to the ground, they have again opposite polarities.

How the active current-to-voltage converter operates (-VIN)

Creating an op-amp inverting current-to-voltage converter

top < prev step - 1 - 2 - 3 - 4 - 5 - 6 - 7 - 8 - 9 - 10 - next step > end

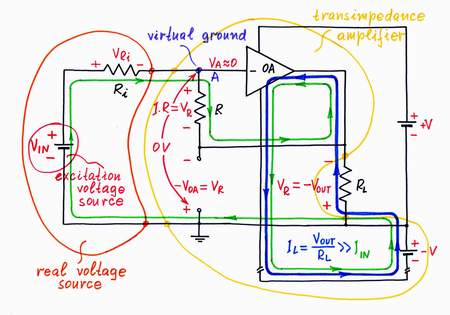
Only, I have got bored of doing this donkeywork; it is beneath my dignity to do it:) Well, I will try to make some electronic device do it; an op-amp seems to be a good choice. For this purpose, I connect the op-amp's output in the place of the helping voltage source and the op-amp's input to point A. As a result, the op-amp compensates the "harmful" voltage drop across the resistor by copying and adding the "copy" voltage to the voltage of the input source (the op-amp produces the compensating voltage VOA = -VR by dosing the voltage of the power supply). Thus, the op-amp "helps" the input source.

Op-amp I-to-V converter = passive I-to-V one + "helping" op-amp

Let's now explore the circuit operation. Again, first imagine that there is not input excitation voltage VIN. As a result, there are not any voltage drops and currents in the circuit; there is almost not a voltage difference between the inverting and non-inverting input of the op-amp. It is "happy" because there is nothing to do:)

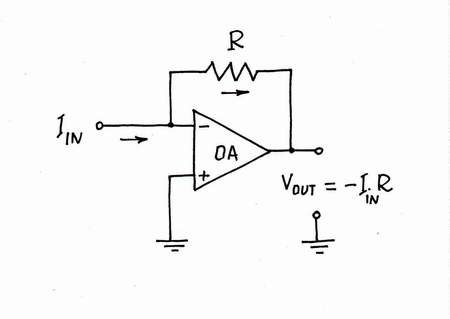
top < prev step - 1 - 2 - 3 - 4 - 5 - 6 - 7 - 8 - 9 - 10 - next step > end

If the input voltage VIN increases, an output current IOUT begins flowing through the resistor R. As a result, a voltage drop VL appears across the resistor and the point A begins rising its potential VA (the input source "pulls" the point A up toward the positive voltage VIN). Only, the op-amp "observes" that to his great displeasure:( and immediately reacts: it decreases its output voltage "sucking" the current IOUT until it manages to zero the potential VA.

Figuratively speaking, the op-amp "pulls" the point A down toward the negative voltage -V to establish a virtual ground. It does this magic by connecting a part of the voltage produced by the negative power supply -V in series with the input voltage VIN. As above, the two voltage sources are connected in series, in one and the same direction (- VIN +, - VH +) so that their voltages are added. Only, regarding to the ground, they have opposite polarities.

Exploring the circuit at positive input voltage

top < prev step - 1 - 2 - 3 - 4 - 5 - 6 - 7 - 8 - 9 - 10 -  next step > end

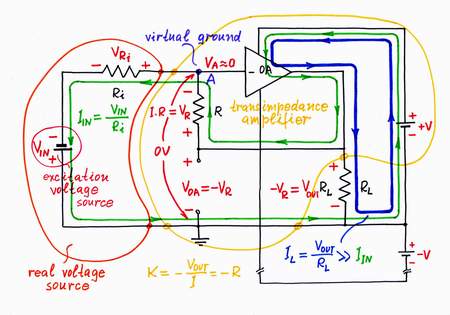
If the input voltage VIN decreases under the ground, an input current IOUT begins flowing through the resistor R in an opposite direction. As a result, a voltage drop VL appears across the resistor and the point A begins dropping its potential VA (now, the input source "pulls" the point A down toward the negative voltage -VIN). Only, the op-amp "observes"' that and immediately reacts: it increases its output voltage "pushing out" the current IOUT until it manages to zero the potential VA.

Now, the op-amp "pulls" the point A up toward the positive voltage +V, in order to establish a virtual ground. It does this magic by connecting a part of the voltage produced by the positive power supply +V in series with the input voltage VIN. The two voltage sources are connected in series again, in one and the same direction (+ VIN -, + VH -) so that their voltages are added. Regarding to the ground, they have opposite polarities as above.

Exploring the circuit at negative input voltage

In the circuit of an op-amp current-to-voltage converter, the op-amp adds as much voltage to the voltage of the input source as it loses across the resistor. The op-amp compensates the local losses caused by this internal resistor (conversely, in the opposite op-amp inverting voltage-to-current converter, the op-amp compensates the losses caused by the external load).

Applications: Staying before the circuit input

Once we created a perfect current-to-voltage converter, we may use it as a building block to build more complex compound circuits. For this purpose, we have only to connect consecutively the separate building blocks. First, we may connect the op-amp current-to-voltage converter before circuits having voltage input; thus we make them perceive current.

top < prev step - 1 - 2 - 3 - 4 - 5 - 6 - 7 - 8 - 9 - 10 - next step > end

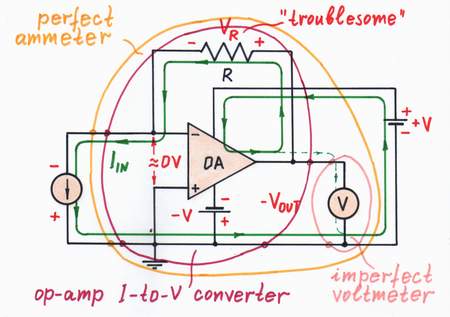
We have already built a simple ammeter by connecting a simple current-to-voltage converter (a shunt resistor) before the voltmeter:

Compound ammeter = current-to-voltage converter + voltmeter

Similarly, we can build a perfect ammeter by connecting an op-amp current-to-voltage converter before the voltmeter:

Perfect ammeter = op-amp current-to-voltage converter + voltmeter

This active ammeter does not introduces a troublesome voltage drop into the measured circuit. Only, the popular multimeters use exactly the passive version, in order to measure big currents (see comparison between the passive and active version ).

Building a perfect ammeter

Applications: Staying after the circuit input

top < prev step - 1 - 2 - 3 - 4 - 5 - 6 - 7 - 8 - 9 - 10 - next step > end

Then, we may connect the op-amp current-to-voltage converter after circuits having current output; thus we make them produce voltage. For example, we have known how to build a simple current source. By applying this technique, we may assemble the famous op-amp circuits of inverting amplifier, capacitive differentiator, inductive integrator, diode antilogarithmic converter, etc.

Op-amp inverting amplifier = V-to-I converter + op-amp I-to-V converter

Op-amp V-to-V CR differentiator = V-to-I C differentiator + op-amp I-to-V converter

Op-amp V-to-V LR integrator = V-to-I L integrator + op-amp I-to-V converter

Op-amp V-to-V DR antilog converter = V-to-I D antilog converter + op-amp I-to-V converter

In all these circuits, the voltage drop across the respective I-to-V converters does not introduce an error (precisely speaking, it introduces an error but the op-amp removes it).

Building various voltage-to-voltage converters

Applications: Acting as a transimpedance amplifier

The op-amp I-to-V converter discussed like as an op-amp V-to-I converter is an active circuit; so, we may expect it to amplify too. Really, it acts as a linear circuit with transfer ratio k = VOUT/IIN [V/mA] or ohms having dimension of resistance. That is why, they frequently name it transresistance or transimpedance amplifier (transimpedance is a contraction of "transfer impedance"). Nevertheless, let's try to answer the question, "Is the op-amp I-to-V converter an amplifier?"

Yes, it is an amplifier! The op-amp inverting I-to-V converter does not consume any power from the input source; it is just a short connection (see the explanations below about the input resistance). So, it is a more perfect amplifier than the opposite op-amp inverting voltage-to-current converter, which consumes power P = VIN²/R. To compare the two circuits, assemble again an op-amp inverting amplifier by connecting consecutively a bare resistor (R1) and a current-to-voltage converter (the resistor R2 and an op-amp OA) - see the figure above.

Comparison between the passive and active version

top < prev step - 1 - 2 - 3 - 4 - 5 - 6 - 7 - 8 - 9 - 10 - next step > end

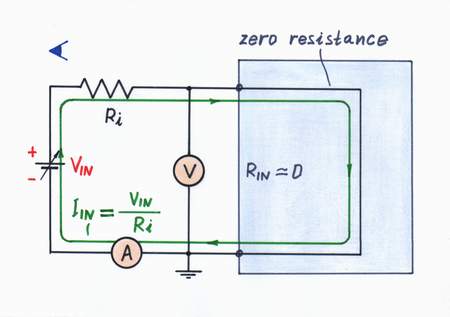
First, connect an ammeter in series with and a voltmeter in parallel to the converter's input; then vary the input voltage to investigate the input resistance. Maybe you remember that in the passive version, looking from the side of the input source we were seeing two resistors connected in parallel - R and RL; so, the input resistance was RIN = R||RL.

Now, we see zero resistance because the op-amp has "neutralized" the resistance R. It is wonderful, the resistor R has disappeared! In this case, the op-amp "helps" the input voltage in its striving to change the current.

What is the input resistance?

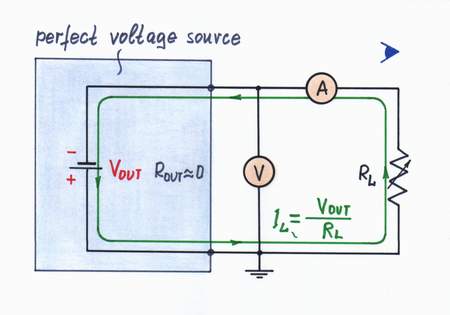
Now, connect a voltmeter in parallel to and an ammeter in series with the converter's output; then, vary the load resistance (voltage) and observe the current to investigate the output resistance. Remember that in the passive version, looking from the side of the load, we were seeing two resistors connected in parallel - Re (the equivalent resistance of the input circuit) and R; so, the output resistance was ROUT = Re||R.

Now, the situation is quite more interesting: when we vary the load the output voltage stays steady! The circuit behaves as a perfect voltage source with zero output resistance.

What is the output resistance?

Operating range. The op-amp does all these "magics" until it can change its output voltage (i.e., until it is within the active region). When it reaches the supply rail, the op-amp saturates, the magic ceases and the almost ideal active circuit becomes again an imperfect passive one. The magnitude of the voltage drop across the load in this moment is referred to as compliance voltage. Note that the passive version does not have such a problem; it is always imperfect:)

Polarities. Another difference between the two versions is that the op-amp circuit is inverting (maybe, in some cases this is an advantage).

Power considerations. Although the active current-to-voltage converter is a perfect circuit, the popular multimeters do not work that way. In order to measure a current, they use the imperfect passive current-to-voltage converter instead of the almost ideal op-amp current-to-voltage converter. The reason for applying such an old-fashioned approach to current measurements is that all the input current IIN flows through the "helping" voltage source BH in the active version. Therefore, the source has to be able to endure such a current. Accordingly, in the practical op-amp circuit, both the power source and the op-amp have to endure the input current measured.

The active (op-amp) current-to-voltage converter is a perfect circuit; however, it is suitable only for low-current applications.

Links to related web resources

Analog electronics 2004:  Class 9 is a teacher's story about the op-amp inverting converters (from the exercices with my students, 2004).

Transimpedance amplifier is a similar but older story.

Op-amp circuit builder shows how to transform any passive converter into an active one (choose the resistor R2 from the library on the right side).

Wikibooks:   Circuit idea - Op-amp inverting current-to-voltage converter reveals the idea behind the active circuit.

                                         Passive current-to-voltage converter reveals the idea behind the passive circuit.

Wikipedia:    Current-to-voltage converter is dedicated to the passive and active versions of the inverse current-to-voltage converter.

                    Voltage-to-current converter  builds consecutively the passive and active versions of the voltage-to-current converter.